Sobre la multiplicación acortada.

El sábado les presenté el método de multiplicación acortada, basado en la sutra de las verticales y cruzados, la cual elimina escribir y hallar dos productos parciales.

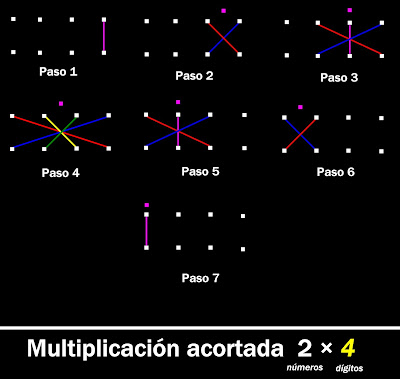
Ésta es la idea detrás de la multiplicación acortada: tratar a cada factor como una secuencia de dígitos, como si fuese una matriz 2 (factores) × n.(dígitos)

Se utiliza con eficacia cuando ambos números tienen dos dígitos o más.

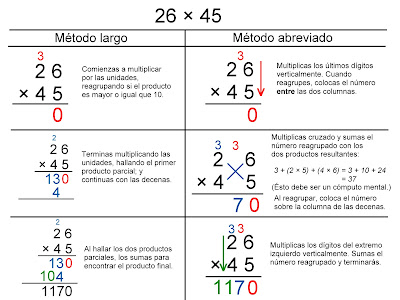
Empecemos multiplicando dos números de dos dígitos y tres dígitos. A continuación les presentamos los pasos a seguir para cada caso:

Es importante recordar que debes dejar buen espacio entre los dígitos para colocar las cantidades reagrupadas del paso anterior. A diferencia de la multiplicación tradicional, que siempre se colocan sobre la columna del número, en la multiplicación acortada habrán ocasiones que la cantidad reagrupada se coloca entre columnas, indicativo que las multiplicaciones que vallas a ejecutar son todas cruzadas; pero cuando está sobre una columna, existirá a lo más una multiplicación vertical, el resto siendo cruzados.

Además, todo cómputo en itálico que ve en los ejemplos son cálculos mentales. La persona que quiera utilizar con efectividad la multiplicación acortada debe dominar las aritméticas mentales.

-------------------------------------------------------------

De seguro habrán notado el patrón en los pasos: moviéndose de derecha a izquierda ocupando poco a poco columnas hasta que las adquiere todas, para luego dejar una por una las del extremo derecho hasta quedarse con la primera desde el extremo izquierdo.Observe la multiplicación de dos factores con 4 dígitos y siga los pasos.

Existe otro patrón: la cantidad de pasos necesarios para hallar el producto:

• dos dígitos = 3 pasos

• tres dígitos = 5 pasos

• cuatro dígitos = 7 pasos

• n dígitos = 2n - 1 pasos

Así podremos generalizar la multiplicación acortada a dos casos: cuando los factores tienen n dígitos impares o n dígitos pares.

Cuando n es impar, al momento de tener todas las columnas ocupadas el dígito a reagrupar estará sobre una columna, indicando que todas las columnas (menos la del medio, Columna # [n + 1]/ 2) se multiplican cruzado con su columna complemento.

Columna #1 con Columna #(n); Columna #2 con Columna #(n - 1); ... ; Columna #([n + 1]/ 2) + 1 con Columna #([n + 1]/ 2) - 1

En el caso de n ser par, todas las columnas se multiplican cruzado con su columna complemento.

Columna #1 con Columna #(n); Columna #2 con Columna #(n - 1); ... ; Columna #([n + 1]/ 2) con Columna #([n + 1]/ 2) + 1 

Otros casos:

• Se puede utiulizar con enteros y decimales.

• Cuando la cantidad de digitos entre factores es dispareja, añades ceros frente al menor hasta que quede parejo:
• 4726 × 53 se escribiría 4726 × 0053.

El Hombre Integral y el uso del comic como método de avalúo en el aula.

Las tirillas cómicas eran lo ue me hacía despertar temprano en las mañanas de domingo (digo hacía, ya que muchos periódicos locales han dejado de publicarlas y/o dejarlas a una sola página llena de crucigramas). Esta mañana me hizo recordar gratos momentos cuando encuentro un comic sobre la integración, expuesto en la página Royst Beef:

El comic escrito en inglés parece haber sido creado como proyecto final de clase, común en escuelas estadounidenses como método de extra crédito. Contiene un dato sobre los integrales (que el área bajo una curva se halla mediante la integración) y un ejemplo aplicado a las leyes superheróicas (hallar el área de una bala, para entonces conocer su punto de vulnerabilidad y el Hombre Integral desintegrándolo con un golpe karateca).

Elementos así hacen el uso del cómic dentro del aula uno enriquecedor, ya que incluyes datos de relevancia (como deficiones, teoremas, postulados) y uno que otro ejemplo; más aún cuando se pueden integrar suavemente en la narrativa (como el de arriba).

-------------------------------------------------------------
Esta es la octava entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Los atajos aritméticos y la multiplicación acortada

Pasando los canales de cable, veo este inusual infomercial sobre un producto para "agilizar la mente" de los estudiantes de primaria en las matemáticas, presentando, en varias viñetas al inventor, preguntándole a los estudiantes que contestaran cuadrados perfectos, y conversiones de fracciones a decimales, hasta seis lugares; con los niños recitándolas en segundos. También salían los testimonios, donde presentaban los métodos, en su mayoría de multiplicación: como hallar el cuadrado de todo número que terminase en 5, multiplicar dos números noventipico, y cosas por el estilo.

Poco a poco me percaté que éstos métodos son solamente atajos aritméticos (todos bajo un término llamado matemáticas védicas), los cuales, en mi opinión, ayudan a que el estudiante aumente su autoestima, elimine sus ansiedades, y tenga una actitud positiva hacia las matemáticas, para que puedan tener un mejor desempeño. En ese punto le veo un propósito al producto. El problema principal es que cae en memorización de casos específicos de multiplicación, en una ruta que pronto se encontrará con variables y ecuaciones.

Eso sí, no todo tema en las matemáticas védicas son solamente para casos específicos. Una de las más conocidas es la de los verticales y cruzados, donde no necesitas escribir los productos parciales de la multiplicación, ya que los estás haciendo mentalmente. Es como la división corta, donde abrevias las restas y escribes el residuo entre los dígitos del dividendo.

La multiplicación abreviada (o acortada) es un método que elimina el escribir los productos parciales, donde se trabaja a los dos factores como una matriz 2 × n, donde n es la cantidad de dígitos mayor entre ambos factores; moviéndose de derecha a izquierda, columna a columna. Es recomendable usarla cuando ambos factores tienen 2 dígitos o más.

Ejemplo: En la multiplicación de dos números con dos dígitos, tenemos la columna de las decenas y la de las unidades, por tanto:

• las unidades del producto se saca multiplicando verticalmente la columna de las unidades de los factores, reagrupando de ser necesario.

• las decenas del producto es el total de los productos cruzados de las columnas y, de haberlo, el número reagrupado.

• las centenas del producto es la multiplicación vertical de la columna de las decenas de los factores

Aquí un caso:

Notarán que el orden en el que se multiplican y se suman los números son idénticos, la única diferencia siendo el método hacia la solución.

La cosa cambia cuando son de tres o más dígitos, donde el algoritmo clásico se descarta y tienes que pensar diferente:

• De derecha a izquierda, trabajas las columnas 2 × n: Supongamos que la columna más a la izquierda es llamada Columna 1, la siguiente Columna 2 y así sucesivamente hasta llegar a la Columna N; y R, el dígito reagrupado. Entonces, el producto tendrá: 
• Unidades: Columna N: verticalmente,
• Decenas: [Columna N y Columna (N - 1)], total de productos cruzados + R,
• Centenas: [Columna N y Columna (N - 2)], cruzados + Columna (N - 1), vertical + R,
• Millares:  [Columna N y Columna (N - 3)], cruzados + [Columna (N - 1) y Columna (N - 2)], cruzados + R, 

Hasta que se utilizan todas la columnas para hallar el próximo dígito:

• Si n es impar: todos cruzados excepto la Columna (N/2):  [Columna 1 y Columna N] +  [Columna 2 y Columna (N - 1)] + ... + [Columna (N/2 - 2) y Columna (N/2 + 2)] + [Columna (N/2 - 1) y Columna (N/2 + 1)] + Columna (N/2), vertical + R,

• Si n es par: todos cruzados:  [Columna 1 y Columna N] +  [Columna 2 y Columna (N - 1)] + ... + [Columna (N/2 - 1) y Columna (N/2 + 2)] + [Columna (N/2 ) y Columna (N/2 + 1)] + R,

Luego de ésto, la cantidad de columnas utilizadas se disminuye, hasta que solamente tengas que multiplicar verticalmente la Columna 1.

Creo que es más facil exponer un ejemplo de dos números, uno de dos dígitos y otro de tres:

En fin, el método acortado de multiplicación requiere pleno poder de las aritméticas mentales. Advierto que este tema es uno puramente recreativo y que si vas a hacer cómputos artiméticos, mejor hacerlos de la manera larga y clásica.

-------------------------------------------------------------
Esta es la séptima entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Cuando te dicen "estudiar religiosamente las matemáticas"...

...no significa algo así:

P.S. Para aquellos que no han utilizado el libro se Stewart, el 5.3 es el Teorema Fundamental del Cálculo.

-------------------------------------------------------------
Esta es la sexta entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Resolver problemas verbales, ¿un arte que pocos cultivan? (Parte II)

Varios factores contribuyen al "odio" que los alumnos le tienen al resolver problemas matemáticos narrados, los comúnmente conocidos como problemas verbales. En la primera parte discutimos como la aversión a dichos problemas sea debido a la ínfima cantidad de problemas que resuelven en su historial académico, dando paso a estudiantes pasivos en razonamiento lógico, reto y rigor matemático; o, de ser activos, una pobre preparación de parte del maestro.

Honestamente hablando la solución de problemas verbales es un tema poco tocado en el aula de clases. Por experiencia propia les puedo contar que la cantidad de problemas verbales (situaciones presentadas en narrativa) que observé dentro de las clases de álgebra y geometría fueron pocas; con el enfoque directo en el proceso enseñanza-aprendizaje de los conceptos discutidos mediante ejercicios.

¿Qué podemos hacer para aliviar la situación?


Primero, el docente, en su rol como estudiante eterno, debe ser un solucionador de problemas verbales activo. De que vale tirar un problema verbal en un examen si nunca los presenta ni ofrece en la clase, Un maestro que está constantemente haciendo en sus ratos libres problemas verbales, va a estar más preparado a integrarlos a sus planes diarios, un ejemplo o dos de análisis de situación.

Segundo, en su rol de liderazgo en el aula, es su deber tener una actitud positiva hacia la solución de problemas verbales y transmitirla a sus alumnos. La causa para que centenares de estudiantes esten lamentandose en la existencia de los problemas verbales puede ser en parte a que el maestro no quiera verlos ni en pintura. El docente debe crear una atmósfera que conduzca al éxito, donde presente la solución de problemas como una ventura excitante, divertida e importante en su desarrollo como seres pensantes. Recuerde, sus acciones dentro del aula lo delatan. Es por eso que debe moldearlas.

Tercero, dejamos algunas recomendaciones, traducidas de la Edición para Maestros de Addison-Wesley Algebra and Trigonometry (1994), que pueden llevar a una aula productiva en la solución de situaciones matemáticas verbales:

• Únase con los alumnos en la experiencia, explorando junto a ellos la situación presentada. Piense en voz alta mientras examina y resuelve. Encomie a los estudiantes a que lo hagan también.

• Demuestre que la solución de problemas es una experiencia diaria mediante la creación de problemas basados en las situaciones de sus alumnos. También que los mismos estudiantres escriban sus problemas.

• De utilizar un libro de texto, personalizar los problemas con elementos locales y los nombres de los estudiantes.

• Reconozca y reenfuerce la voluntad y la perseverancia.

• Recompense a aquellos que toman riesgos.

• Encomie a los estudiantes a utilizar corazonadas y acepte soluciones inusuales.

• Enfatice la persistencia y creatividad sobre la velocidad.

• Haga que los estudiantes analicen sus soluciones; y muestre que la verificación e interpretación son parte del proceso de solución. Además que escriban explicaciónes de como llegaron a esa conclusión.

•  Integre información sobre inventos y noticias como ejemplos solución de problemas en la rutina diaria.

Ahora, lea el siguiente problema verbal (presione la imagen):

El acercamiento para resolver el problema  se hace en cuatro fases (las cuales expliqué brevemente en la Parte I):

• Resumir: Sacar en síntesis los detalles de relevancia del problema (datos explícitos e implícitos), entendiendo la cuestión que se nos pide; preferiblemente en sus propias palabras.

• Plantea: Delinear la(s) estrategia(s) a utilizar para resolver el problema:
• Escribir una ecuación / inecuación
• Dibujar una diagrama
• Tanteo
• Encontrar un patrón / secuencia
• Hacer una tabla
• Resolver por secciones / resolver un problema más fácil
• Trabajar en reversa
• Utilizar el razonamiento lógico

• Resuelve: Ya escogida y expuesta la estrategia, muestras los pasos y procesos utilizados hacia la solución.

• Contesta: Tras verificación e interpretación, presentas la solución en oración completa y con las unidades de medidas correspondientes (de tenerlas)

Veamos una de las posibles rutas hacia la solución.

Recuerde que el problema no termina en dar la contestación correcta. Este es el comienzo para que discuta otras estrategias que hayan utilizado otros alumnos, la creación de problemas derivados del resultado, o la exploración de un tema nuevo.

En fín, si los maestros ponemos actitudes positivas hacia la solución de problemas e intentamos convertirlo de una actividad pasiva a una activa, podremos cambiar las actitudes que los estudiantes tienen hacia éstas; de esta manera cultivando la semilla del reto, razonamiento y análisi matemático.

-------------------------------------------------------------
Esta es la quinta entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

La demostración geométrica de un producto de Cauchy

(1 - 1 + 1 - 1 + ...)² = 1 - 2 + 3 - 4 +...

imagen via [The Math Kid]

La mejor demostración es aquella que puede ser visualizada, como las sumatorias demostradas por geometría que presentamos hace dos Carnavales atrás. De esta manera podemos atraer más personas al lado demostrativo, el lado menos visto de las matemáticas.

-------------------------------------------------------------
Esta es la cuarta entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Las metas del maestro de matemáticas, según French (1881)

Éste extracto, traducido de un escrito de John H. French para Elementary Arithmetic for the Slate (1881), menciona cuatro metas que todo docente matemático debía tener:

1. Impartir instrucción nueva y valiosa, adaptada por tipo y cantidad, a la condición mental de nuestros pupilos;


2. Enseñar a los pupilos a razonar, para así guiar sus propias investigaciones y descubrir las verdades por sí mismos;


3. Hacerlos concienzudos, al requerirle recitaciones y explicaciones precisas, y;


4. Mantenerlos interesados es sus estudios.

En 131 años, el rol del maestro ha evolucionado a niveles inimaginables, pero todavía se ven presentes éstas cuatro metas dentro del aula.

[via]

-------------------------------------------------------------
Esta es la tercera entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Sentido común vs análisis matemático

¿Cree poder hallar en menos de 10 segundos la cantidad de regiones que formarían seis puntos unidos?

En el texto de Geometría de la Serie Matemática Moderna se nos presenta esta situación para que el alumno pueda ver como el sentido común (la primera intuición que la persona tiene hacia un problema, muchas veces de facil solución) nos puede traicionar y darnos una respuesta incorrecta.

El alumno que se va por el sentido común notará al instante que existe un patrón multiplicativo en la cantida de regiones formadas: 2^(n - 1); por tanto diciendo que seis puntos unidos dentro de un círculo formarán 32 (2^5) regiones. Pero al analizar más allá de cómputos y concentrándonos en la hacer la figura, notarán que no formaría dicha cantidad. Y como no especifica si el hexagono formado es regular o irregular, existirían dos soluciones diferentes.

Eso sí, la única forma que pudiese sacarlo en 10 segundos por sentido común correctamente es que supiese de antemano sobre grafos completos de n vértices y la fórmula para sacar la cantidad de aristas formadas, la cual es la misma fórmula de Gauss utilizó para sumar números consecutivos cuando tenía 6 años.

-------------------------------------------------------------
Esta es la segunda entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Resolver problemas verbales, ¿un arte que pocos cultivan? (Parte I)

Durante toda la semana, se ha rondado en las redes sociales una imagen similar a la que presento arriba, donde generalizan al problema verbal de matemáticas como una inentendible verborrea donde lo que relata y la respuesta no tiene nada en común con la pregunta principal y la información provista.

Entonces, ¿a que se debe esta reacción negativa a la matemática narrativa?

Una de las varias razones para que ocurra semejante hecho es debido a que existen muchos alumnos que durante el transcurso del año escolar solucionan una ínfima cantidad de problemas verbales. Así, cuando le ponen un problema verbal de frente, se paniquean. Se agrava la situación cuando la preparación que ofrece el docente para resolver dichos problemas es una paupérrima, sin rigor, razonamiento y/o reto matemático. Estudiantes que se les hace dificultoso los problemas verbales matemáticos piensan que todos los datos están presentes en la información; y vaticinan que el resultado puede ser sacado por sentido común, mediante el machacamiento de cómputos. Pero más importante, no pueden traducir la información del lenguaje hablado a la matemática. Es el arte matemático que pocos dominan y muchos evitan cultivar.

Si Joaquín Monserrat "Pacheco", eterno presentador infantil de Puerto Rico, natural de Barcelona, estuviese con nosotros, daría el consejo de la imagen para todo atleta, sea deportivo y/o académico.

• Resolver problemas verbales toma bastante práctica, ya que debes construir la habilidad de reconocer lo que pide el problema, datos explícitos e implícitos, y conocimiento previo que hagan conectar la información provista con una solución. 

• Recuerda: Resume la situación presentada, Plantea tu estrategia de solución, Resuélvelo con todos los pasos lógicos y Contéstalo en oración completa. 

• Debes estar activamente resolviendo acertijos y problemas, acrecentando el rigor y nivel de razonamiento y análisis lógico, crítico y matemático de vez en cuando.  

• Acuérdate que, como los atletas olímpicos, dominar una destreza toma tiempo y esfuerzo.  

• No te desanimes ni te rindas si no te sale el problema. Hasta los mismos matemáticos se han tardado años en resolver problemas. Si se te hace dificil hallar la solución de un problema, descansa tu cerebro un rato y ten un momento de ocio. Quizás la solución salga cuando menos lo esperas.

Éste sería el grano de arena que debe aportar el alumno para un mejor desempeño en la resolución de problemas verbales matemáticos; ya que el maestro trae consigo éstas y otras responsabilidades; las cuales hablaremos en la segunda parte.

-------------------------------------------------------------
Esta es la primera entrada hecha para la Edición 3.1415 del Carnaval de Matemáticas, cuyo anfitrión en esta ocasión es el blog Gaussianos.

Hace tres décadas atrás: la computadora en el aula de matemáticas

Estados Unidos, 1982. Se estaba comenzando a impulsar  el método de solución de problemas en el aula de matemáticas, junto con la visualización de aplicaciones en los diversos campos de trabajo. Como suplemento, se proveían actividades con las calculadoras científicas de bolsillo, la novedad a la vuelta de la esquina. Y, si tenían los recursos suficientes, se les enseñaba el lenguaje BASIC para realizar simulaciones.

Para principios de los años ochenta uno de los intentos para propiciar el uso de la tecnología en la población estudiantil fue el integrar la creación de programados computadorizados en los cursos matemáticos. Los libros de texto proveían suplementos que explicaban flujogramas y lectura y escritura del BASIC, junto con dos o tres programas a ejecutar.

Les presento un ejemplo:

Imágenes generadas por computadora y la familiar fuente de ordenador que se utilizaba en los ochenta engalanan las portadas de éstos tres textos. Como parte de mi biblioteca, poseo el de Álgebra y Trigonometría; y puedo decirles que en cada capítulo existe una actividad para utilizar el lenguaje BASIC, sea para completar una tarea matemática o una aplicación de ésta al mundo laboral. Veamos algunos de los programados que presenta.

Verificar si un binomio en particular es factor de un polinomio de cuarto grado.

Determinar si la raíz cuadrada de una fracción es racional o irracional.

La secuencia Fibonacci hasta T términos. Incluye instrucciones para hacer la proporción áurea.

Aplicación de la función de seno.

Si regresamos al presente verán que al pasar el tiempo, con el progreso de la tecnología se crearon otros lenguajes que simplificaron estas tareas (LOGO, C, C++,...) hasta se pudieron hacer con simplemente una hoja de datos (spreadsheet), una calculadora gráfica o el Internet; pero es importante poder regresar al pasado y ver como era el papel de la tecnología digital de entonces y reflexionar en que en tres décadas se hablará de lcomo la tecnología del presente es arcaica.

El porqué será dificil que el libro de texto impreso se esfume

Hace tres semanas atrás visité el Salvation Army más cercano y me encontré con la sorpresa del siglo: una carpa llena de cajas conteniendo libros. Más aún cuando estaban vendiendolos en paquetes de diez por un dólar, una excelente manera de crear tu propia bliblioteca referencial sin gastos excesivos. Mientras me aventuraba en explorar las cajas de textos escolares, revistas y tomos, me puse a pensar sobre el final de la era del libro impreso.

Como sabemos, la fiebre de los e-books y sus lectores, con la capacidad de almacenar todo un anaquel completo en la palma de la mano, está en su apogeo, dándole un aviso de muerte al libro tradicional. La pregunta es, ¿cuánto tiempo le queda a texto en papel? ¿Se hará una transición directa, o una co-existencia híbrida?

Curt Hopkins ha escrito un artículo (para Ars Technica) que muestra con pruebas la posición y el destino del libro impreso en la educación moderna, llamándolo persistente y terco, evitando declarar al e-book como el próximo paso de la lectura por un tiempo. Leanse hasta los comentarios.

Todo se ha movido exitosamente al mundo en línea: desde la guía telefónica hasta la enciclopedia. Pero la terquedad del libro impreso siempre estará presente, ya que siempre existirán piezas literarias que probablemente nunca se volverán a imprimir o transferir digitalmente. Éstas joyas son las razones para decir que será dificil la desaparición del libro impreso. Les dejo la imagen como muestra, el tesoro más grande que me llevé del botín de aquel día de abril.

RLFB XXIX: Empujándonos el difícil a lo que ya es difícil

• Imagen: Un interesante concepto, pero le cambiaría el subtítulo a "Master of logic and numbers" (aunque sabemos que las matemáticas cubre muchísimo más). [via]

• Referente al título de la entrada: El Gobernador de Puerto Rico quiere para el 2022 se ofrezcan todas las clases (salvo Español) en inglés. Este reto es uno cuesta arriba, ya que: 
• no se ha enseñado de esta manera desde 1948; 

• menos del 1% de las escuelas públicas tienen un currículo completamente en inglés

• significaría certificar que cada maestro domine el idioma (tanto en el sentido gramatical como en la conversacional).

• Más aún, ¿cómo vamos a empujar las clases en el lenguaje inglés, si tenemos muchos jóvenes que fallan en escribir correctamente ensayos y resumés en español?

• Desde el tintero de Randall Munroe: xkcd ha presentado tres excelentes tirillas durante las pasadas semanas: una sobre aproximaciones numéricas a constantes conocidas, otra diciéndonos que todas las concentraciones son terribles, y un comentario sobre la enseñanza del álgebra.

• "♪♫Que bonita bandera...♫♪": ...es la bandera puertorriqueña, especialmente cuando exploramos su geometría. Si lo sé, le falta color.

• Devorando fractales: Desayuna pancakes en forma de constantes matemáticas y fractales.

• Algo que no cambia: los precios de las calculadora gráficas de antaño.

• Demostrando la creatividad matemática:  el súeter de factorización prima de Sondra Eklund; utilizar una naranja para ilustrar una espiral de Euler.

• Debate educativo: Más artículos para reflexionar sobre varios temas educativos-matemáticos:
• Scott Schneider argumenta que las Ciencias de Computación NO son matemáticas.

• Edudemic presenta una lista con los 20 elementos más disruptivos dentro de la educación de hoy.

• La naturaleza de las matemáticas vs. la naturaleza de la educación matemática.

La escuela del mañana ha existido por unos años...

La escuela del mañana

panel del comic Closer Than We Think (Mas cerca de lo que pensamos) de Arthur Radebaugh

(domingo 5 de mayo del 1958)

imagen via [1950sunlimited]

Fíjese en la imagen y póngase a pensar cuáles de los elementos presentados aparecen ahora mismo en el aula de clases; más aún si han sido mejorados de una forma u otra. Verá como hemos, en tan poco tiempo, superado las expectativas. Eso si, pasará tiempo en que toda escuela pueda estar al día.

P.S. En la computadora con la solución del ejercicio, falta el exponente ⁿ de afuera en el paso del medio.

Física sayajin

imagen via [educomunicar]

Como entiendo un poco de portugués, creo que lo puedo traducir:

"Goku es un super sayajin, que en sus horas libres entrena sus poderes en un local bastante distante de la ciudad en donde vive. Imagínese que un día el lanzó una esfera de 10 kg de masa que se mueve a una velocidad constante de 20 m/s. El valor de la energía cinética de la esfera luego de 9 segundos de movimiento vale:" 2000 J

Un día para celebrar y reflexionar (RLFB XXVIII)

La primera semana de mayo se celebra en Puerto Rico la Semana Educativa, donde el jueves o viernes se hace el Día del Maestro. Es la primera vez que lo celebro, pero desde el desempleo. Pero que todavía no he tenido el placer de estar a cargo de un grupo de estudiantes (fuera de la tutorías y la Práctica Docente) en un salón de clases, no quiere decir que esté inactivo.

Me puse a leer varios artículos interesantes sobre educación y matemáticas que deseo compartir:

• Los 30 mejores maestros de todos los tiempos: El título parace ser elaborado como una listado de personas que trascendieron culturas y tiempos y tuvieron un gran impacto en la educación de hoy, pero lo que presenta Dave Stopera son 30 razones de que el maestro puede ser gracioso y un humano normal.

• La predicción del Wikipedia: Bob Stein, quién trabajó en Atari y la Enciclopedia Britannica, en conjunto con Alan Kay y el ilustrador Glenn Keane presentaron hace 30 años atrás la idea de una enciclopedia inteligente, una computadora que te diría sobre terremotos, la bolsa de valores e historia desde la plama de tu mano.

• Artículos de opinión: El propósito de la educación en el siglo XXI; Las cinco peores cosas que un maestro le puede decir a sus estudiantes; los libros de texto se van a ir por el mismo camino que las páginas amarillas.

• La marcha de la muerte científico-matemática: Este término fue creado por el profesór emérito de ingenieria David E. Goldberg para presentar la realidad del cambio inmediato que muchos alumnos universitarios en la nube STEM tienen que lidiar: un tornado de cálculo, física y química en un gran salón con cientos de estudiantes, diferente a los laboratorios de nivel secundario. El artículo de The New York Times recalca que por este repentino cambio, ocurre un 40% (60 si incluímos pre-médica) de cambios de concentración o baja de parte del estudiantado STEM; con diferentes razones propuestas.

• ¿Estamos enseñando la matemática de la manera que no es?: Richard Rusczyk, el maestro de matemáticas detrás de The Art of Problem Solving, añade una razón adicional al problema presentado en el artículo anterior: La educación matemática estadounidense tradicional no es retante y basada en memorización.

• Para despedirme, un consejo: Dejen de decirle a los estudiantes que estudien para pasar el examen. En éste artículo del Chronicle les dice el porqué.

Felicidades a todos los educadores del mundo en su día.