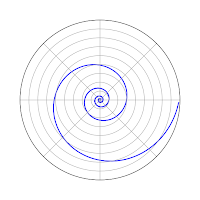
Ahora bien, muchos tenemos la costumbre de creer ciegamente que toda espiral que se encuentra naturalmente comentamos sin demostración que es de Fibonacci, y la encajamos el rectángulo áureo en todas las espirales que vemos como si fuera la zapatilla de cristal de Cenicienta en los pies de las hermanastras, cuando muchas veces se queda corto en uno de los lados (queda chico) o sobrepasa uno de los lados (es más larga). Es por estas razones que les presento la verdadera espiral que se encuentra en la naturaleza, la espiral logarítmica.
La ecuación que produce la espiral logarítmica es
r = ae^(bθ)
r : radio
a & b: constantes positivas
θ : ángulo alrededor del origen
¿Dónde encontramos la espiral logarítmica?
En animales, vegetales, hasta en fenómenos naturales, espaciales y fractales. Quizás las vimos como espiral Fibonacci sin saber.
La próxima vez que estemos presentando las espirales, recuerde la de Fibonacci, pero reconozca a la espiral logarítmica común. Hay que cuestionar siempre los misterios de la naturaleza y no solamente realizarlos porque se asemeja o se acerca bastante.
Si quieren más información al respecto a dicho misticismo, lean éste ensayo escrito por Donald Simanek.
Fotos e información via [Proof]@Tumblr















No comments:
Post a Comment